These are Rheotomic Surfaces – from the Greek
Rheo – flow
and
Tomos – cut or section (as in tomography)
The horizontal sections of these surfaces correspond to the moving equipotential lines of a 2D Laplacian flow, with height mapped to time. Such surfaces are complete, embedded and walkably connected.

In this essay I present a type of mathematically generated surfaces with some unique geometric properties making them particularly well suited for architectural use.
I also present some interesting by-products from the development of these surfaces including a novel and simple way of making conformal grids from flows without the usual methods of vector field integration.
Finally, I suggest some possible directions for the future development of these ideas, both in architectural and purely geometric fields.
In their 1960s work on ‘The function of the oblique’ Claude Parent and Paul Virilio proposed a new architecture of habitable circulation based not on the horizontal and vertical but on the slope. They sought to remove the distinction between floorspace and vertical circulation elements such as stairs.
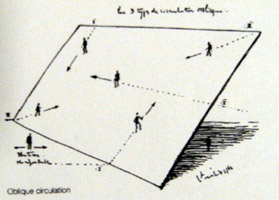
‘the last element to be revealed in architecture will be the floor’. That is the key. Architecture has always been about the wall, the column, the roof… The thing that is overlooked is the floor… Architecture in this sense becomes choreographic. Its value comes only from the fact that it engages the body in the same way that the great staircases of Palladio engage the body. Somehow that is architecture.

…it was necessary to discard the notion of vertical enclosure, whose walls are made inaccessible by gravity, and to define habitable space by means of wholly accessible inclined planes, thereby increasing the usable surface areas.

…In contrast to partitions or vertical walls, which provoke an opposition between in front and behind, a combination of oblique and horizontal planes would result only in above and below, surface and soffit.
By setting the structure on an incline, and making every part of the built surface (except for the underside) habitable and accessible, the range of truly habitable spaces would be considerably increased.
The Function of the Oblique, Claude Parent and Paul Virilio
I was inspired by the potential these ideas had for the creation of a dynamic and highly 3-dimensional architecture, but saw several problems with their application as shown in the sketches. Namely: the awkward acute spaces under some of the slopes, the large steep areas, and the lack of structural rationale. All these issues are addressed by rheotomic surfaces.
There has been a surge of curved surface and ‘single-surface’ architectural schemes over the last couple of decades. This has been partly driven by the capabilities of modern 3D softwares, but is also often tied to the theories of Deleuze about smooth vs. striated space.
There has also been a growing appreciation of the structural potential of doubly curved surfaces, as exploited by Candela’s thin concrete shells for example.
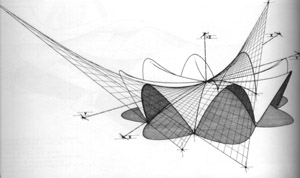
Modern knowledge of these surfaces owes a great deal to the work of the mathematical giants Riemann and Gauss. Their ideas of manifolds and curvature have fundamentally changed some of our ways of thinking about space, and play an important part in Einstein’s theories of relativity. If an architecture is to express a worldview then it seems natural to seek an architecture which embodies some of these ideas.
One area of mathematics which has advanced dramatically since the advent of computers is the study of minimal surfaces (surfaces with zero mean curvature, as approximated by soap films) .
The newfound ability to visualize these surfaces has enabled the discovery of many beautiful new examples. Their appearance can provoke a fascinating sense of solid/void dichotomy.
Images of these surfaces have naturally caught the attention of architects, and attempts to use them in the design of buildings go at least as far back as the 1970s (see Pearce and Gabriel). Minimal surfaces which form repetitive 3-dimensional structures – the Triply Periodic Minimal Surfaces(TPMS) such as the Gyroid and its associate P and D surfaces have recieved particular attention. However, attempts at an architecture based on these concepts have so far been been held back by a number of factors:
One is the daunting nature of the mathematics involved. The growing popularity of parametric modeling has meant that architects are now often quite comfortable with surfaces that can be generated from a simple function giving x y z in terms of u and v, but rarely when faced with something more advanced like the Weierstrass elliptic functions used in minimal surface mathematics.
Another problem is their symmetry. Most known minimal surfaces are either single inviolable entities or they are made up of endlessly repeating identical units. To be useful for architecture a geometric system needs a degree of flexibility, the ability to adapt to varied inputs.
One possible approach is to simply reject mathematical purity and take some of the techniques for working with curved surfaces and apply them in a free-form manner. But if the architect does not have real control of the tools he uses, the work is merely a collage or imitation, and without the integrity of the maths behind it, design quickly gets into difficult waters regarding structural performance and buildability.
As the great physicist Richard Feynman said:
..”the Great Architect seems to be a mathematician”. To those who do not know mathematics it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature … Physicists cannot make a conversion to any other language. If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in. She offers her information only in one form; we are not so unhumble as to demand that she change before we pay any attention.
While it can be taxing, the benefits of using this language can be huge and often unexpected. In his famous essay on The Unreasonable Effectiveness of Mathematics in the Natural Sciences Eugene Wigner talks of the apparently miraculous way that maths sometimes seems to give more back out than we put in:
the enormous usefulness of mathematics in the natural sciences is something bordering on the mysterious and there is no rational explanation for it. […] the mathematical formulation of the physicist’s often crude experience leads in an uncanny number of cases to an amazingly accurate description of a large class of phenomena. This shows that the mathematical language has more to commend it than being the only language which we can speak; it shows that it is, in a very real sense, the correct language.
One area in which this unreasonable effectiveness, this magic manifests itself most strikingly is in the plane of complex numbers – created by combining the real number line with factors of i, the square root of minus one.
The introduction of these ‘imaginary’ quantities seems odd, even nonsensical at first, but for such a simple idea few inventions can rival it for the astonishing richness of worlds which have sprung from it and the vast range of applications it has found in mathematics, and also in descriptions of natural phenomena.
Indeed there is now hardly an area of modern physics which does not depend in some fundamental way upon the use of complex numbers.
One of the particularly elegant and beautiful places these magical numbers appear is within the world of Complex Analytic functions.
Harmonic functions are those which satisfy Laplace’s equation:
where is the Laplacian
Some elementary solutions are:
The point Source:
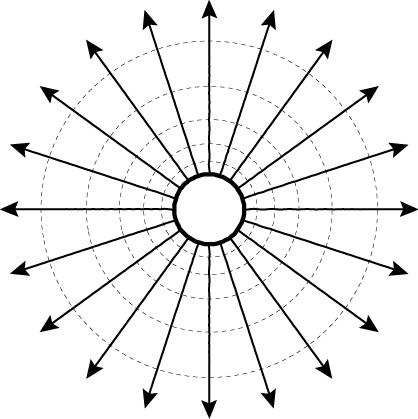
Velocity potential Stream function
and the Vortex:
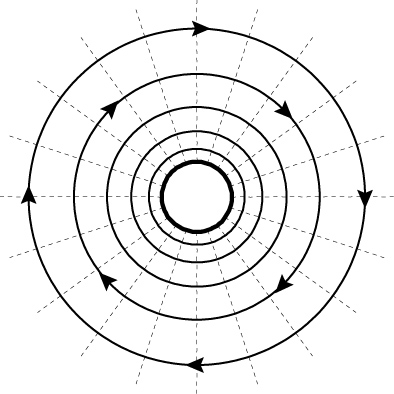
Velocity potential Stream function
Because Laplace’s equation is linear, combinations or superpositions of these solutions are also solutions.
When I was exploring various geometric shapes during my architecture studies I started to use the technique of tomography (imaging of 3D objects through sectioning, often used medically).
In particular, I found it useful to make tomographic animations of objects – taking one of the 3 physical dimensions of space and mapping it to time to give a moving 2-dimensional picture which fully describes the form of the object.
This technique arose naturally when faced with the challenge of making architectural drawings of a building with no flat floors and no vertical walls. The plan is different for every small change in height so one has to show the continuous change.


Starting from a realisation that I could take helicoids and chop and mirror them to form a surface, I used these tomographic animations to develop a theory of walkable connectedness.
One of the other problems with most other designs using smooth or minimal surfaces has been that although the surface is continuous, one often cannot get from one point to another on the surface without going upside-down somewhere in between.

This leads to absurdities such as these floating stairs in Toyo Ito’s Taichung Opera House…


…and holes needing rails to stop people falling down them, and generally makes the the curved surface begin to seem more like a problem than a solution.
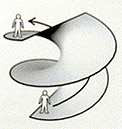
The usefulness of the helicoid in the spiral stair is due to the fact that although it covers the same disc of horizontal space at many heights, they are connected in a walkable way. This is precisely the quality which rheotomic surfaces exploit – by making an equivalence between the vortex in Laplace’s equation and the helicoid surface we can use the principle of superposition to build up any arrangement of clockwise and anti-clockwise helicoids, and join them smoothly into one continuous surface.
Simply put, two points are walkably connected if one can draw a curve on the surface between them along which top and bottom at never switch places.
Looked at in terms of tomographic animation, the problem of the overhangs in surfaces such as those made by joining planes with catenoids is equivalent to the movement of the contour stopping and reversing direction.
To keep the parts of the surface walkably connected, the movement of the contours must always continue to flow.
Tomographic animation of the surface shown in the flythrough at the top of the pageUsing Laplace’s equation makes it possible to generate a smooth continuous surface without ever having overhangs. At the singularites of the flow the surface turns vertical, but because this is a single point in plan, there is never an edge to fall off. The most direct route down is always on the surface.
This is also very useful structurally, as it means loads can always be passed down into the surface. Indeed a rough test running these structures through an FEA structural analysis program indicated that the loads tend to get passed down towards the vertical axes of the helicoids.
Recalling the problems with the oblique architecture referred to at the start we can now see that they are all solved by rheotomic surfaces :
No acute spaces – The floor to ceiling height is everywhere constant.
Fewer steep areas – The average gradient becomes vanishingly small the larger the area of the surface considered (in fact the gradient at any point is inversely proportional to its horizontal distance from the axis)
Structural rationale – Development is still needed here, but initial indications are that their mathematical properties give them an intrinsically structural quality.
To summarise :
Rheotomic surfaces combine useful and dynamic architectural form with structural performance.They do so through some of the most beautiful and profound ideas in modern mathematics.
They utilize advanced geometry not just as a fancy roof or a decorative pattern, but as the fundamental generator of an exciting new type of space, one which avoids many of the common pitfalls and provides a viable alternative to the flat parallel and orthogonal planes of architecture based on the Cartesian box.
————————————–
By-products and future directions of development
Conformal maps
One of the advantages of pursuing a mathematical method of design is that you sometimes get to reap the benefits of its unreasonable effectiveness.
After realising that the streamlines and equipotentials of Harmonic flows were the answer I had been looking for in my development of these surfaces, there was a long period during which I tried to find ways of generating them.
I found various applets which could show a vector field as a grid of arrows, and some which would allow me to plot individual streamlines starting from any point. But none of the tools I found gave me the evenly spaced lines I wanted.
I developed a fascination with the strange beauty of conformal maps, with their curvilinear squares, but the only examples I could find of these were for highly regular arrangements.
So I set out to make my own tool for generating these. Using various tools and languages (such as Generative Components, Rhinoscript, Processing and Grasshopper) I looked in vain for a way to make these curves. Research suggested that I was going to have to learn about vector field integration techniques, which range from the simple but crude Euler method to the more accurate but worryingly difficult sounding 4th order Runge-Kutta method.
But then I realised that it was possible to generate the surfaces directly, which gave beautiful conformal maps ‘for free’ so to speak, from the sections of the surface.
These arrangements of mutually perpendicular curves are very interesting in their own right. Various engineers have looked at using these lines because of their ability to model the principal stresses in a structure.
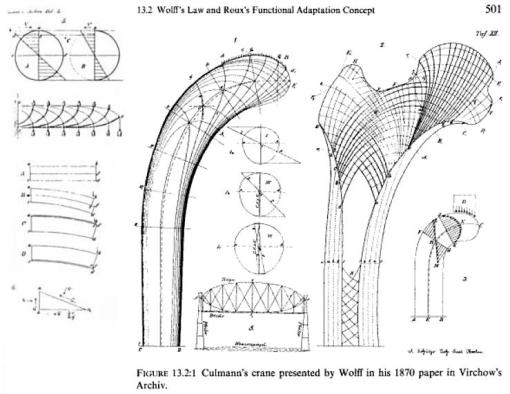
In On Growth and Form, D’Arcy Wentworth Thompson refers to the example of Culmann’s crane, whose form was inspired by the curves in a section of trabecular bone. Also, Michell trusses – certain ‘ideal’ structures arising through a process of topological optimisation exhibit this characteristic arrangement of curved lines.

Perhaps most famously, Pier Luig Nervi used these ‘lines of force’ in the reinforcement pattern for the ceiling of his Gatti Wool Mill. Using my technique it should be possible to calculate such grids for an irregular arrangements of supports:


Circle Packings

I found that there also appear to be some interesting circle packings connected with these patterns.
I think some of the most interesting architectural geometry research of recent years has been in the areas of discrete minimal surfaces, PQ meshes, conical meshes, Laguerre geometry etc. Most of this work seems to be happening at TU Wien and the Geometry Group at TU Berlin.
Principal curvature lines and circle packings play an important role in some of this work and I have a hunch that my current work might relate to this in interesting ways, which I would like to explore further.
(I think there might also be a generalisation of Doyle spirals here)
Structural performance
Rheotomic surfaces certainly appear to have some very useful structural qualities, but it is obvious that in their pure form as described here they do not deal with loads in an ideal way, as they become asymptotically planar far from the vortices. Perhaps they could be optimised in a catenary fashion, or maybe combining sources with each vortex would help give the necessary curvature.
Non-orientability
One issue not addressed so far here is the way space is divided by the surface into 2 separate volumes, and the surface into 2 walkably connected areas. This is an outcome of the mathematical fact that any surface without edges or self intersections must be orientable. One simple way to deal with this might be to join the surface in parts with helicoids at half the vertical scale, thus making it non-orientable and fully walkably connected. I will provide illustrations of this shortly.
Moving vortices
Rheotomic surfaces are not in general minimal surfaces, as they contain vertical lines at each vortex, and any minimal surface with straight lines must be symmetric with respect to 180 degree rotation about that line. Certain arrangements are very closely related with minimal surfaces, and Matthias Weber and Martin Traizet have explored some of these in this paper
So far I have considered the vortices to be stationary, but it might be interesting to consider how they are themselves moved by the flow.
(as described here)
For example a pair of counter rotating vortices will propagate in a straight line, (which would give a surface more like Riemann’s minimal surface) and a pair of similar vortices would circle around each other (twisting the surface to become more like the helicoid with handles).
Vortices in higher dimensions
Instead of looking at flows caused by arrangements of singularities in 2 dimensions, I thought it would be interesting to look for equivalent 3-dimensional vortices. Instead of points, one then has lines and circles about which the space revolves. I began to explore this a bit in my post here, using stereographic projection in 4D. Things rapidly become rather confusing, with the non-commutativity of rotations, one gets into spinors and double covers. Instead of complex numbers, quaternions seem to be the natural language for such explorations.
Harmonic Duals

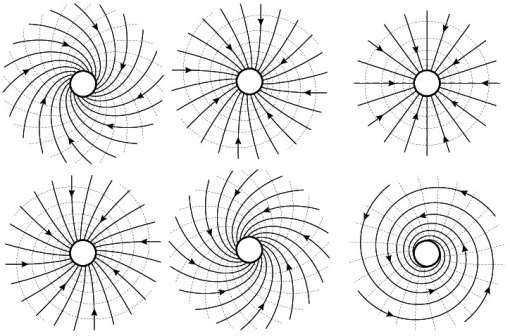
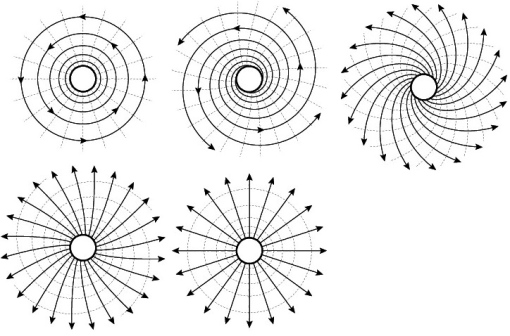
It is interesting to see how by varying one parameter we can continuously change a source into a clockwise vortex, into a sink, into an anti-clockwise vortex and back again.
Here I must refer to the beautiful book Visual Complex Analysis by Tristan Needham. This book has inspired my explorations more than any other.
Finally, I end with an observation of the visual connection with John Whitney’s incremental drift as shown in the Whitney Music Box
Except where otherwise noted, content on this site is licensed under an Attribution-Noncommercial-Share Alike 3.0 Creative Commons License

April 21, 2009 at 8:32 pm
[…] Rheotomic Surfaces […]
April 23, 2009 at 12:21 pm
great piece of information.. thanks for sharing
May 23, 2009 at 6:08 pm
[…] Rheotomic Surfaces […]
September 7, 2009 at 1:17 am
[…] more info: rheotomic surfaces […]
October 1, 2009 at 6:26 pm
[…] one of my images inspired by Daniel Piker’s studies with conformal mapping & field lines. Post a Comment or Leave a […]
April 8, 2010 at 9:19 am
Interested follower …
August 23, 2010 at 1:56 pm
[…] rheotomic-surfaces: spacesymmetrystructure […]
December 16, 2010 at 10:56 pm
[…] https://spacesymmetrystructure.wordpress.com/rheotomic-surfaces/ […]
December 17, 2010 at 12:34 am
[…] https://spacesymmetrystructure.wordpress.com/rheotomic-surfaces/ […]
July 8, 2011 at 8:38 am
First of all, thanks for the hard work on all the things you’re putting out there for everyone to use (like Kangaroo!). In terms of abstract geometry this rheotomic surface stuff is great! (It must be, because I don’t really understand most of the mathematical relationships you refer to.) I would imagine someone at UNstudio is working hard on appropriating your research :)
Here’s the thing I can’t get out of my mind, though :
Even though the geometry you’re able to produce solves the circulation problem evident in Ito’s Opera House (and it wouldn’t take too much effort at all to get some stairs on there), can this approach be adapted to meet universal accessibility requirements without losing it’s mathematical purity?
In other words, if we legally need a 4 to 5 slope on some of the helicoids, and are quite happy with a 30 degree slope on most of the rest, but really also want a 20 or 15 degree circulation surface in situations that call for it… can this diversity be accommodated with a constant floor-to-ceiling height space without increasing the thickness of the horizontal part of the surface?
To shift it out of the pragmatic into the conceptual realm, you’ve nailed the biggest problem with Virilio+Parent’s proposition – it’s a call for a universal space which, even though it is determined primarily by flows and movement, requires a lot of effort to be occupied to the fullest potential; physical effort on part of the subject, nonetheless. Your solution/development certainly relaxes the form with respect to how it is experienced, but still seems kind of limiting as to who is permitted to experience it.
Contemporary architecture needs egalitarian spaces that permit difference, in order to really be worth the money and effort of building something. (imho)
July 8, 2011 at 11:57 am
Thanks Ivan for a really interesting comment,
You raise good point about the gradients and their relation to floor-ceiling height.
If you keep within the pure geometric system, the slope is directly tied to distance from the vertical axes. So can get down to 4 degrees or whatever you need if you make the surface large enough horizontally (in relation to floor-ceiling height).
For example, with a floor to floor height of 3m, all parts of the surface more than about 7m away from a vertical axis would have a slope of less than 4 degrees.
I think to really make it a practical and architecture with a wide range of applications, one would need to look at many ways of cutting into the system, and perhaps mixing and connecting systems of different vertical scales.
This is just as with buildings based on evenly spaced orthogonal and parallel planes, where the pure system is usually not strictly adhered to everywhere, but cut into with all sorts of offsets, atria, double height spaces etcetera.
It is this sort of creative variation within and beyond the pure system that takes it beyond just geometry and into architecture.
July 8, 2011 at 4:09 pm
[…] Rheotomic Surfaces « Space Symmetry Structure: “Modern knowledge of these surfaces owes a great deal to the work of the mathematical giants Riemann and Gauss. Their ideas of manifolds and curvature have fundamentally changed some of our ways of thinking about space, and play an important part in Einstein’s theories of relativity. If an architecture is to express a worldview then it seems natural to seek an architecture which embodies some of these ideas. […]
July 8, 2011 at 4:36 pm
awesome. particularly that last video.
September 3, 2011 at 9:29 am
[…] Rheotomic Surfaces […]
November 8, 2011 at 12:42 am
Grat work. Congratulations!
June 13, 2013 at 7:48 am
It’s fun to delve into the black box here since it’s open source and has lots of internal Grasshopper structure. Alas, how do I also output your circle packing example, I wonder? These curve networks seem to match a very old Macintosh screen saver called Flowfazer created by rock star Todd Rundgren that was recently re-released as an iPhone app. Back in 1990 it was rather ahead of its time indeed!
August 27, 2013 at 8:24 pm
Cool page. Wish you had included the equations as well.
May 15, 2014 at 7:15 pm
[…] Rheotomic Surfaces […]
January 29, 2015 at 5:52 pm
Just desire to say your article is as amazing. The clearness for
your submit is just nice and i could think you are knowledgeable in this subject.
Well with your permission let me to clutch your feed to keep updated with impending post.
Thanks 1,000,000 and please keep up the enjoyable work.
April 22, 2017 at 5:05 am
[…] 部分文字图片来源参考自:https://spacesymmetrystructure.wordpress.com/rheotomic-surfaces/ […]
September 25, 2017 at 3:13 pm
[…] James – paper on the British Museum, Daniel Piker’s blog on Rheotomic Surfaces […]
July 1, 2018 at 9:10 am
Daniel you are my hero! I really enjoyed reading your explanation on Rheotomic surfaces. I was able to hack your script and create a free-form start-up work environment with integrated furniture all based on this pure geometrical equation! This video shows an animated section of my design. https://www.youtube.com/watch?v=-RryWwPVuLA. In addition, I was able to put my design in VR and truly experience this oblique landscape. There are still many challenges, but actually seeing the visual connectivity created by the shape and the atria’s (also based on the equation) was a very unique and beautiful experience.
February 20, 2019 at 12:59 pm
[…] James – paper on the British Museum, Daniel Piker’s blog on Rheotomic Surfaces […]