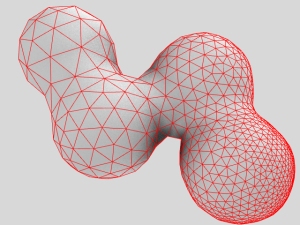
As regular readers of this blog will know, I’m passionate about the use of relaxation and force-based methods for optimizing geometry in a very interactive way.
There is a great variety of form-finding that can be done by assigning physical forces as interactions between sets of particles. However, in my investigations so far, the topology of these interactions has usually remained fixed. So the overall shape changes dramatically, but the number of points -and the underlying network of which point interacts with which- remains the same throughout the simulation.
I have written about topology optimization before, in my post on self organizing structures, but the videos above use a fundamentally different approach than any of the examples shown there, as this new work is based on purely local interactions, which reconfigure their connectivity as the geometry changes.
I did experiment a while back with a different technique for dynamic remeshing based on repelling/colliding particles or spheres (see this video, skip to around 1:27 for the mesh generation), but this was limited by a number of factors – although the spheres only exert force on each other when they are closer than a certain distance, they still need to be constantly checked against all the other spheres to see if they are within this distance. Checking every sphere against every other one means the number of interactions increases as the square of the number of particles, which becomes slow for even modest meshes of a few thousand vertices.
There are various ways of significantly reducing this complexity and cutting down the number of distance calculations to be performed at each iteration (such as partitioning the space into cubic cells, and only checking for interactions between particles in the same or neighbouring cells). However, there still remains the question of how to remove or add spheres if they get too close or too spread out. Then even when a fairly equal distribution of points across the surface has been achieved, turning this into a clean mesh can still be tricky.
Instead, using the mesh connectivity itself from the very beginning as the network of which vertices interact with which, and updating it iteratively and locally based on its changing geometry, solves all of these problems at once. This connectivity update can be done by using repetitions and combinations of just 3 essential moves :
edge flip
edge collapse
edge split
(or alternatively, one can use edge flip, vertex insertion and vertex removal)
vertex insertion/removal
I’m always using a triangulated mesh here. In the 2nd and 3rd videos at the start, the underlying physics is still working with triangles, but I’ve shown the dual of this, which exchanges the roles of faces and vertices, turning a mesh of mostly triangles into one of mostly hexagons:
Notice that the irregular vertices of the triangle mesh (ones which have 5 or 7 connected edges instead of the regular 6) correspond to pentagons and heptagons in the dual. Finding the right number and placement of these irregular vertices is an important part of making a good mesh. There is a close relationship between these irregular vertices and the overall topology and curvature of the mesh. Euler’s polyhedron theorem gives us a precise relationship between the number of faces/edges/vertices, and the genus of the mesh (F-E+V=2-2g). This is linked to Descarte’s polyhedron theorem, which relates the total angle defect at the vertices to the genus, and is itself a discrete version of the continuous Gauss-Bonnet theorem which describes a similar relationship for the integral of Gaussian curvature in the smooth case.
Keeping a good quality triangular mesh (close to even sized equilateral elements, with no obtuse, skinny or degenerate ones) can be very useful for many other types of optimization and simulation, as well as an advantage for fabrication if it is to be built as a physical structure.
I’m thinking I could also vary the remeshing rules depending on whether the priority is regularity of geometry, or regularity of connectivity. For example, on a sphere, a geodesic dome has a small number of irregular vertices (this is sometimes referred to as a semi-regular mesh), but a fair amount of variation in edge length, whereas solutions to the Thomson or Tammes problems reduce the variation of distance, but have larger numbers of irregular vertices.
If the triangles all have identical edge lengths, then all of the angle defect is concentrated at the irregular vertices, whereas if the edges can vary slightly, the angle defect can be spread out across the mesh. As mentioned above, by Descarte’s theorem, the total angle defect is fixed, but if the number of vertices is increased it can be divided between more of them. Subdividing each triangle (using a smoothing scheme such as Loop subdivision) does not alter the configuration of irregular vertices, but reduces the angle defect at each vertex (and in the smooth limit it approaches zero as the number of vertices approaches infinity).
The remeshing can also be based on other criteria than just equal triangles. Reducing triangle size in high curvature areas is an obvious one, but I have a hunch there could also be some interesting ways of basing it not just on geometry, but on stresses, and using it for structural optimization.
I find remeshing fascinating because the same geometric rules and operations have relevance across so many different disciplines and at a variety of scales.
For example, in the carbon nanostructures graphene and nanotubes, which are hexagonal arrangements of atoms, there is a much studied crystallographic defect which occurs called the Stone-Wales defect – where instead of all hexagons we get 2 pentagons and 2 heptagons. It has important implications for the material’s mechanical and electrical properties. If we look again at our edge-flip move on a regular triangular mesh, and its effect on the dual, we see that it is exactly the Stone Wales defect!
There are even hypothetical carbon nanostructures (proposed by Mackay and Terrones) in the shape of doubly curved triply periodic minimal surfaces known as Schwarzites.
(from the paper Curved nanostructured materials)
As the bond lengths between the Carbon atoms are very rigid, the only way these curved structures can be formed is through the variations in mesh connectivity.
Because such complex geometries are only dependent on the way in which many identical elements are connected, rather than variation in the elements themselves, they can be modelled using simple materials (no laser cutting involved – just clever assembly!):
(by Bih-Yaw Jin from the beaded molecules)
(by Dimitry Tishchenko)
(by Loop.ph)
Going down to even smaller scales, we can even find the use of similar ideas about mesh connectivity in theories of loop quantum gravity, spin foams, and Regge calculus (for example, see Canonical Simplicial Gravity by Dittrich and Höhn, or The Feynman diagramatics for the spin foam models). Pachner moves or bistellar flips generalize the mesh moves described earlier to higher dimensional simplices.
(images from Canonical Simplicial Gravity)
So as well being potentially useful for design, meshes and their properties have profound relevance to our understanding of the nature of space and curvature, because of the way they link the discrete and the continuous.
I’ll be continuing to work on these remeshing tools and their combination with other types of relaxation and optimization. These recent developments are not publicly available for now, but I’ll update here with any news.
Here are a few more references on remeshing:
Dynamic Remeshing and Applications
A Remeshing Approach to Multiresolution Modeling
__________________________
also – a general update : Around a year ago I started working full time for Foster+Partners in the Specialist Modelling Group. This has been a really great experience, working on (and applying Kangaroo on) some big and exciting projects, but core Kangaroo development (and posts here) did necessarily slow down a bit during this time. However, I have recently left F+P and things will be changing ! More news to follow…